Lexicon of Statistical Modelling
and Related Topics
Compiled by
C. Patrick Doncaster
Compiled by
C. Patrick Doncaster

Contents
ADDITIVITY. The assumption that interaction is not present between ANOVA main effects. This assumption must be made in any GLM design in which there is only one variate per treatment combination, because interactions cannot be tested in the absence of replication.
AKAIKE INFORMATION CRITERION. A criterion for assessing the relative fit of competing models. AIC = 2 x (model performance log-likelihood + number of parameters estimated). Smaller values of AIC indicate a closer fit of the model to the data.
ANALYSIS OF COVARIANCE. (ANCOVA). A technique used in experimental designs that have both categorical and continuous explanatory variables. An ancova tests a dependent variable for homogeneity among categorical group means, after using linear regression procedures to adjust for the groups' differences in the independent and continuous covariate. In experimental designs the covariate is usually a nuisance variable. When it is not, in analysis of observational data, a GLM approach can be adopted. Ancovas make all the ASSUMPTIONS of parametric analysis of variance; they additionally assume linearity of the regression, and no treatment by slope interaction.
ANALYSIS OF VARIANCE. (ANOVA). A technique for partitioning sources of variance
in a continuous response variable into variance among (between) groups and
variance within groups (the error variance). One use of analysis of variance is
to test whether two or more sample means from different levels of a treatment
could have been obtained from populations with the same parametric mean
(one-way anova, H0: variation in the response variable is not
due to the treatment). A one-way anova computes a value of F from the
ratio of the between-group mean square to the within-group mean square. A
significant difference between groups is indicated by a larger value of
F than the critical value for a chosen 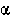 in tables of the
F distribution, with a-1 and n-a degrees of freedom
for n subjects in a groups. The mean squares, which estimate each
source of variance, are computed from the SUM OF SQUARES divided by the degrees
of freedom for that source. A multi-way anova computes a value of F for
each main effect, and for INTERACTIONS between main effects (if there are
replicate observations of main effect combinations). Appropriate care must be
taken to meet the ASSUMPTIONS of analysis of variance, and to use the correct
ERROR term and DEGREES OF FREEDOM. In general, an analysis of variance approach
is used to test for dependency of the response variable (Y) to one or
more qualitative (categorical) independent variables or treatments
(Xi). If the independent effects are quantitative
(continuous), then a REGRESSION approach is adopted. A GLM can use either or
both types of independent variable, as can an ANALYSIS OF COVARIANCE.
in tables of the
F distribution, with a-1 and n-a degrees of freedom
for n subjects in a groups. The mean squares, which estimate each
source of variance, are computed from the SUM OF SQUARES divided by the degrees
of freedom for that source. A multi-way anova computes a value of F for
each main effect, and for INTERACTIONS between main effects (if there are
replicate observations of main effect combinations). Appropriate care must be
taken to meet the ASSUMPTIONS of analysis of variance, and to use the correct
ERROR term and DEGREES OF FREEDOM. In general, an analysis of variance approach
is used to test for dependency of the response variable (Y) to one or
more qualitative (categorical) independent variables or treatments
(Xi). If the independent effects are quantitative
(continuous), then a REGRESSION approach is adopted. A GLM can use either or
both types of independent variable, as can an ANALYSIS OF COVARIANCE.
ASSUMPTIONS OF PARAMETRIC ANALYSIS OF VARIANCE. All types of parametric analysis of variance (ANOVA, REGRESSION, ANCOVA, GLM) make six general assumptions about the data. They assume (i) that subjects are sampled at random (S'), and (ii) that the response variable has a linear relationship to any quantitative effects. They make three assumptions about the characteristics of the error term in the model. The error, or `noise,' stands for all the variables influencing the response variable that have been omitted from the analysis, plus measurement error in the response variable. These assumptions are: (iii) the error terms in the response are normally distributed about the main effect means; (iv) the error terms are independently distributed, they succeed each other in a random sequence so that knowing one is no use in knowing the others; (v) the error terms are identically distributed for each treatment level, giving homogeneous variances. A final assumption is made when each combination of two or more effects has only a single observation (so there is no replication), (vi) that the main effects are additive (no interaction). Several of these assumptions can be met by TRANSFORMATION of the variables. Non-independence is a problem that often arises because of shared links between data points that are not admitted in the analysis. Use either mean values or BLOCKS to remove nuisance dependencies such as adjacent time intervals in time series, or siblings among subjects. REPEATED MEASURES of a subject also violate the assumption of independence, unless this is acknowledged in the choice of error term. For any nested design, care must be taken in constructing the proper F-ratio to avoid PSEUDOREPLICATION. Good experimental design involves choosing in advance the optimum balance of treatment levels and sample sizes to provide sufficient power for testing the hypotheses of interest. See Methods: Analysis of variance for examples of anova designs.
BERNOULLI TRIALS. Repeated independent trials are called Bernoulli trials if there are only two outcomes for each trial and their probabilities remain the same throughout the trials (e.g. tossing a coin). The probabilities of the two possible outcomes are written as p (success) and q (failure), and p + q = 1. The sample space for an experiment consisting of n Bernoulli trials contains 2n points. Since the trials are independent, the probabilities multiply, so the probability of the outcome sffs is given by pqqp. Where one is interested in the total number of successes in a succession of Bernoulli trials, but not in their order, then the probability of Y successes in k trials is given by the BINOMIAL DISTRIBUTION.
BINOMIAL DISTRIBUTION. A discrete probability distribution measuring the relative frequencies of (0,k), (1,k-1), (2,k-2), ...(p,q)... (k,0) occurrences of two alternative states (e.g. male, female) in a sample of size k, expected for given parametric proportions of p and q. The general formula for any term of the binomial distribution is C(k, Y)pYqk-Y, where C(k, Y) is the number of combinations that can be formed of k items taken Y at a time. On the assumption of a true ratio of alternative states (e.g. sex-ratio of 1:1), the probability of obtaining an observed deviation from this ratio (e.g. 12M:3F) is calculated from the relative expected frequency of the observed outcome, plus all outcomes that are even more unlikely than that observed. If this probability is very small, then one or more of the following assumptions is unlikely: (i) that the true ratio is that which had been assumed (1:1); (ii) that sampling was at random in the sense of obtaining an unbiased sample; (iii) that the alternative states (sex of offspring) are independent of each other (although the average ratio is 1:1, individual litters may be largely of one sex or the other). Unlike the chi-squared test, binomial tests can be one-tailed, i.e. testing for directional bias.
BLOCKS. In GLM, blocks are groups of subjects which are more homogeneous, in the absence of any treatment effect, than they would be had they been assigned to groups at random. Blocking is a useful way to partition out the effects of nuisance variables, such as time, sex or siblings which would otherwise violate the assumption of INDEPENDENCE. A Latin square design is used for the case where two nuisance variables need to be blocked simultaneously. This is a pattern in which each of n levels of a treatment is represented once in each column and once in each row of a square matrix of n blocks (levels) of nuisance factor A by n blocks of nuisance factor B. This provides orthogonal contrasts and removes the effects of A and B prior to testing the effect of the treatment.
CANONICAL ANALYSIS. This is the most general of the multivariate techniques. Canonical models have several variables on each side of the equation, and the goal is to produce, for each side, a predicted value (dimension) that has the highest correlation with the predicted value (dimension) on the other side. The fundamental equation for canonical correlation can be represented in matrix form by the product of the four correlation matrices: one between dependent variables (Ryy, inverted), one between independent variables (Rxx, inverted), and the two between dependent and independent variables (Ryx , Rxy). Thus:
R = (Ryy-1Ryx)(Rxx-1Rxy)
The two components of this equation can be thought of as regression
coefficients for predicting X's from Y's, and regression
coefficients for predicting Y's from X's (the latter being
equivalent to Bi in the COEFFICIENT OF DETERMINATION.
The next step is to redistribute the variance in the matrix R in order
to consolidate it into a few pairs of canonical variates from the many
individual variables. Each pair is defined by a linear combination of
independent variables on one side and dependent variables on the other, and
should capture a large share of variance, determined by the squared canonical
correlation rci2 (called the eigenvalue,
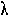 i, for the pair of canonical variates). Canonical
correlation, rci, is then interpreted as a product-moment
correlation coefficient.
i, for the pair of canonical variates). Canonical
correlation, rci, is then interpreted as a product-moment
correlation coefficient.
CENTRAL LIMIT THEOREM. As sample size increases, the means of samples with finite variances, drawn at random from a population of any distribution, will approach the normal distribution. This result explains why the normal distribution is so commonly used with sample means. The theorem leads directly to the formula for the STANDARD ERROR OF THE MEAN.
CHI-SQUARED 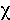 2. A statistic used in tests of significance relating
to tables of frequencies, where it has a probability distribution approximately
that of a sum of squares of several independent N(0,1) variables (i.e.
variables with a mean of zero and a variance of 1). The distribution assumes
truly categorical data and independent frequencies (the occurrence of an event
ij is not influenced by the type of the preceding event).
2. A statistic used in tests of significance relating
to tables of frequencies, where it has a probability distribution approximately
that of a sum of squares of several independent N(0,1) variables (i.e.
variables with a mean of zero and a variance of 1). The distribution assumes
truly categorical data and independent frequencies (the occurrence of an event
ij is not influenced by the type of the preceding event).
COEFFICIENT OF DETERMINATION. r 2. This is the square of the correlation coefficient. It is the ratio of the explained sums of squares of one variable to the total sums of squares of the other. It is thus a measure of the proportion of the variation of one variable determined by the variation of the other. In REGRESSION analysis, it measures the proportion of the total variation in Y that has been explained by the regression. In multiple regression, the coefficient of determination can be represented in matrix form by:
r 2 = RyiBi
where Ryi is the row matrix of correlations between the dependent variable and the k independent variables, and Bi is a column matrix of standardised regression coefficients for the same k independent variables. The standardised regression coefficients are obtained by inverting the matrix of correlations among independent variables, and multiplying it by the column matrix of correlations between the dependent variable and the independent variables:
Bi = Rii-1 Riy
COMBINATIONS. The number of combinations that can be formed of n items taken r at a time (no repetitions, order not important): C(n, r) = n! / [r!(n-r)!]
CONFIDENCE LIMITS. Regardless of the underlying distribution of data, the
sample means from repeated random samples of size n will have a
distribution that approaches normal for large n, with 95% of sample
means at µ ±1.960 (for large sample sizes). Having
computed the sample mean
(for large sample sizes). Having
computed the sample mean 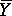 and standard error, we can state that these
are our best estimates of the parametric mean µ and standard deviation
and standard error, we can state that these
are our best estimates of the parametric mean µ and standard deviation
 , and compute 95% confidence limits for µ at
, and compute 95% confidence limits for µ at 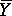 ±1.960.SE (for large sample sizes). The 99% confidence limits for
µ are at
±1.960.SE (for large sample sizes). The 99% confidence limits for
µ are at 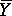 ±2.576.SE. For small sample sizes, confidence limits
for µ are computed at
±2.576.SE. For small sample sizes, confidence limits
for µ are computed at 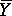 ±t.SD/
±t.SD/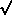 n. For a
linear regression y = b0 +
b1x, 95% confidence limits for the slope are obtained
at b1 ± t[.05]n-2
SEb1. Confidence limits for a proportion are computed
from cumulative binomial probabilities. For the computation of confidence
intervals to a ratio of two proportions, see RISK RATIO.
n. For a
linear regression y = b0 +
b1x, 95% confidence limits for the slope are obtained
at b1 ± t[.05]n-2
SEb1. Confidence limits for a proportion are computed
from cumulative binomial probabilities. For the computation of confidence
intervals to a ratio of two proportions, see RISK RATIO.
CONSERVATIVE TEST. A test is conservative if the stated level of significance is larger than the actual level of significance, or the stated confidence intervals are too broad. In other words, the risk of making a type I error is therefore not as great as it is stated to be. The test is too severe.
DEGREES OF FREEDOM. The number of dimensions required to define location. In an
ANOVA, the dimensions that make the group means differ provide the test
dimensions, while those corresponding to variation within groups (a pure
measure of the random component since all plots given the same treatment are
treated alike) provide the benchmark dimensions. The degrees of freedom are the
numbers of pieces of information about the `noise' from which an investigator
wishes to extract the `signal.' When sums of squares are divided by n-1
rather than by n the resulting sample variances will be unbiased
estimators of the population variance,  2. The only
time when division of the sum of squares by n is appropriate is when the
interest of the investigator is truly limited to the sample at hand and to its
variance and standard deviation as descriptive statistics of the sample, in
contrast to using these as estimates of the population parameters. For goodness
of fit tests, expected frequencies based on an intrinsic hypothesis result in
an extra degree of freedom being removed for each parameter calculated from the
data (e.g. the fit of observed frequencies to a normal distribution, which is
computed with the mean and SD of the data, would be tested with a chi-squared
for a-3 d.f.; a-2 for Poisson and binomial, where a is the
number of samples). Linear REGRESSIONS are calculated with n-2 d.f.
because it takes two points to make a straight line. For a GLM model the
degrees of freedom are multiplied up from the sources of variance contributing
to the mean square, using number of levels for sources inside parentheses and
number of levels minus 1 for sources outside. So the nested effect
A'(B) has (aj -1)b d.f.; and its error
term: S'[A'(B)] has (ni
-1)ajb d.f., for ni subjects per level
of A and aj levels of A per level of B
and b levels of B. The cross-factored error effect
S'(AB) has (ni - 1)ab = n -
ab d.f.
2. The only
time when division of the sum of squares by n is appropriate is when the
interest of the investigator is truly limited to the sample at hand and to its
variance and standard deviation as descriptive statistics of the sample, in
contrast to using these as estimates of the population parameters. For goodness
of fit tests, expected frequencies based on an intrinsic hypothesis result in
an extra degree of freedom being removed for each parameter calculated from the
data (e.g. the fit of observed frequencies to a normal distribution, which is
computed with the mean and SD of the data, would be tested with a chi-squared
for a-3 d.f.; a-2 for Poisson and binomial, where a is the
number of samples). Linear REGRESSIONS are calculated with n-2 d.f.
because it takes two points to make a straight line. For a GLM model the
degrees of freedom are multiplied up from the sources of variance contributing
to the mean square, using number of levels for sources inside parentheses and
number of levels minus 1 for sources outside. So the nested effect
A'(B) has (aj -1)b d.f.; and its error
term: S'[A'(B)] has (ni
-1)ajb d.f., for ni subjects per level
of A and aj levels of A per level of B
and b levels of B. The cross-factored error effect
S'(AB) has (ni - 1)ab = n -
ab d.f.
ERROR. The amount by which the observed value differs from the value predicted by the model. Also called residuals, errors are the segments of scores not accounted for by the analysis. In analysis of variance, the error term is the denominator of the F-ratio, and contains all of the mean square components of variance that are in the numerator except the one component of variance that is being tested.
ERROR STRUCTURE. Describes the distribution of the variance remaining after testing for an affect. Many kinds of ecological data have non-normal error structure: e.g. skewed, kurtotic, or bounded data. This can be dealt with by transforming the response variable or using non-parametric statistics. In GLIM, however, it is possible to specify a variety of different error distributions (see LINK FUNCTION).
FIXED EFFECTS. For levels within a treatment to be considered fixed, the levels must be repeatable if the experiment were to be performed again. The conclusions reached about fixed effects are valid only for the specific levels used in the experiment. See also RANDOM EFFECTS.
GENERAL LINEAR MODELS. (GLM). A comprehensive set of techniques concerning how a continuous response variable is determined, predicted or influenced by a set of independent variables. ANOVA, ANCOVA and REGRESSION are all special cases of glm. A glm makes the same ASSUMPTIONS as an anova, but it can be used with non-orthogonal main effects, unbalanced designs and main effects that are continuous as well as categorical. See ORTHOGONALITY and MARGINALITY for correct interpretation of adjusted and sequential sums of squares in the glm tables. A post-hoc glm (as opposed to an experimental design) should be treated as a multiple regression if possible, i.e. with continuous fixed effects, so it will not then be necessary to declare the full model (undeclared sources of variance thereby contributing to the error). For categorical response variables see LOG-LINEAR MODELS and LOGISTIC REGRESSION.
GENERALISED LINEAR MODELS. (GLIM). A program to fit linear models. A linear model is an equation containing mathematical variables, parameters and random variables, that is linear in the parameters and in the random variables. GLIM is used to specify a statistical model for a data set, to find the best subset from a set of models, and to assess the goodness of fit and display the estimates, standard errors and predicted values derived from the model. A GLIM has three properties: the ERROR STRUCTURE, the LINEAR PREDICTOR, and the LINK FUNCTION.
| 1. |  |
 |
alpha | 9. |  |
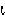 |
iota | 17. | 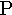 |
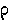 |
rho |
| 2. | 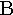 |
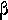 |
beta | 10. | 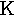 |
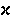 |
kappa | 18. | 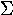 |
  |
sigma |
| 3. |  |
 |
gamma | 11. |  |
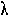 |
lambda | 19. | 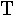 |
 |
tau |
| 4. | 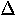 |
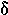 |
delta | 12. |  |
µ | mu | 20. |  |
 |
upsilon |
| 5. |  |
 |
epsilon | 13. |  |
 |
nu | 21. |  |
 |
phi |
| 6. | 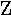 |
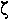 |
zeta | 14. |  |
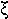 |
xi | 22. | 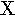 |
 |
chi |
| 7. |  |
 |
eta | 15. |  |
 |
omicron | 23. | 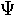 |
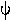 |
psi |
| 8. | 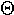 |
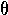 |
theta | 16. |  |
 |
pi | 24. | 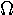 |
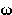 |
omega |
HYPERGEOMETRIC DISTRIBUTION. A distribution equivalent to the binomial case but sampled without replacement and from a finite population (i.e. not a random sample, but a complete set of observations on some population). The individual terms of the hypergeometric distribution are given by the expression:
C(pN, r)C(qN, k-r) / C(N, k)
which gives the probability of sampling r items of the type represented by probability p out of a sample of k items from a population of size N. The hypothesis of independence or randomness in a two-way table of frequencies with fixed marginal totals induces this probability distribution. Fisher's exact test is based on this distribution. If the same row and column variables are observed for each of several populations, then the probability distribution of all the frequencies can be called the multiple hypergeometric distribution. Randomised blocks use this distribution.
INDEPENDENCE. In linear models the assumption of independence refers to the random component of the model: y = systematic component + random component. The systematic component allows y to depend on the x-variables; it is specified by intercepts, slopes and group differences, and is tested against the random component. Data points are said to be independent of each other if knowledge of the random component of one is completely uninformative about the random component of any of the others. BLOCKING for nuisance variables is a common way of removing dependency from the random component.
INTERACTION. An interaction term is significant in a GLM when the effect on the response variable of one independent variable is modulated by another independent variable. Interaction terms are described by products in model formulae, and they are related to the main effects by considerations of MARGINALITY. In an ANOVA, a first order interaction can be visualised as the separation of group means between the levels of X1 having a different pattern at different levels of X2. In ANCOVA, this is equivalent to a significant difference between the slopes of two or more regression lines representing the predicted relationship of Y to continuous X1 at each level of a categorical variable X2 (could be ordinal treated as categorical). In REGRESSION, two continuous variables have a significant interaction effect when the slope of the plane in X1 is different to the slope in X2. In contingency tables, the null hypothesis of independence between column and row classifications is rejected if the cell frequencies indicate a significant interaction between the categories.
LEVELS. A treatment in ANOVA will have at least two levels within it. Levels can be thought of as degrees or categories of a treatment.
LIKELIHOOD FUNCTION. Used in estimating values of the parameters in a GLIM (see MAXIMUM LIKELIHOOD ESTIMATORS). The likelihood function is the same as the joint probability density function of the response variables (Yjk, e.g. the weight of the kth individual from the jth sample where j = 1 for control and 2 for treatment). But it is viewed primarily as a function of the parameters, conditional on the observations yjk, whereas the joint probability density function is regarded as a function of the random variables Yjk (conditional on the parameters).
LIKELIHOOD RATIO STATISTIC. 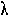 . A measure of goodness of fit of a
chosen GLIM to the data. This is accomplished by comparing the likelihood under
the model with the likelihood under the maximal (saturated) model. The
maximal model is a GLIM using the same distribution and link function as the
model of interest, but the number of parameters is equal to the total number of
observations, n. It therefore provides a complete description of the
data for the assumed distribution. The likelihood functions for both models are
evaluated at the respective maximum likelihood estimates, and
. A measure of goodness of fit of a
chosen GLIM to the data. This is accomplished by comparing the likelihood under
the model with the likelihood under the maximal (saturated) model. The
maximal model is a GLIM using the same distribution and link function as the
model of interest, but the number of parameters is equal to the total number of
observations, n. It therefore provides a complete description of the
data for the assumed distribution. The likelihood functions for both models are
evaluated at the respective maximum likelihood estimates, and 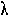 is obtained from the ratio of one to the other. Equivalently, the
LOG-LIKELIHOOD RATIO is obtained from the difference between the log-likelihood
functions.
is obtained from the ratio of one to the other. Equivalently, the
LOG-LIKELIHOOD RATIO is obtained from the difference between the log-likelihood
functions.
LINEAR PREDICTOR. The structure of a generalised linear model relates each observed y-value to a predicted value. The predicted value is obtained by transformation of the value emerging from the linear predictor. The linear predictor is a linear sum of the effects of one or more explanatory variables, xj. In a simple REGRESSION, the linear predictor is the sum of two terms: the intercept and the slope. In a one-way ANOVA with four treatments, the linear predictor is the sum of four terms: the mean for treatment 1 and the three differences of the other treatment means when compared with treatment 1. If there are covariates in the model, they add one term each to the linear predictor. To determine the fit of a given model, GLIM evaluates the linear predictor for each value of the response variable, then compares the predicted value with a transformed value of y. The transformation to be employed is specified in the LINK FUNCTION.
LINK FUNCTION. The link function relates the mean value of y to its LINEAR PREDICTOR in GLIM. Examples of link functions are the identity link (for normal errors, where the linear predictor = µ), log link (for count data with Poisson errors), logit link (for proportional data with binomial errors: logistic regression), reciprocal link (for exponential errors, useful with survival data on time to death). The value of the linear predictor is obtained by transforming the value of y by the link function.
LOGISTIC REGRESSION. A type of log-linear analysis used in modelling a dependent variable of proportion data, where the responses are strictly bounded between 0% and 100%. The logistic curve, unlike the straight-line model, asymptotes at 0 and 1, so that negative proportions and responses > 100% cannot be predicted. Uses a LOGIT LINK FUNCTION for binomial errors. Explanatory variables are generally continuous; for categorical factors, consider a LOG-LINEAR model of a contingency table with two columns (Success and Failure).
LOGIT FUNCTION. The logarithm of the ODDS RATIO, or log[ i
/(1-
i
/(1- i)], for i binomial distributions
B(ni,
i)], for i binomial distributions
B(ni,  i), having
i), having
 i probability of an event occurring. This is the
appropriate link function for proportional data, with binomial errors. For a
logistic model with categorical effects, the parameter, l, for each cell
can be converted to an odds ratio with the equation: odds ratio =
e2l. This is the a priori odds for a parameter,
and it is multiplicative among parameters. See also RISK RATIO.
i probability of an event occurring. This is the
appropriate link function for proportional data, with binomial errors. For a
logistic model with categorical effects, the parameter, l, for each cell
can be converted to an odds ratio with the equation: odds ratio =
e2l. This is the a priori odds for a parameter,
and it is multiplicative among parameters. See also RISK RATIO.
LOG-LIKELIHOOD RATIO. STATISTIC (DEVIANCE). Given by D = 2 log
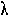 , where
, where 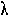 is the LIKELIHOOD RATIO. This
statistic is used for testing the adequacy of a GLIM. The difference in
deviance between two competing models approximates a
is the LIKELIHOOD RATIO. This
statistic is used for testing the adequacy of a GLIM. The difference in
deviance between two competing models approximates a 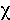 2
distribution with d.f. given by the difference in the number of parameters
(N-p). Thus larger values of D suggest that the model of
interest is a poor description of the data. See also AKAIKE INFORMATION
CRITERION.
2
distribution with d.f. given by the difference in the number of parameters
(N-p). Thus larger values of D suggest that the model of
interest is a poor description of the data. See also AKAIKE INFORMATION
CRITERION.
LOG-LINEAR MODELS FOR CONTINGENCY TABLES. Used for analysing contingency tables by means of a generalised linear model with a log link function. In a two-way table of counts, a chi-squared test is used to ask the question: is there any association between row and column factors? This can be rephrased as: does the distribution of ratios in the different columns vary from one row to another? This is then a question of interaction in a GLIM, from which can be derived a linear predictor for the logs of the expected frequencies. The log link ensures that all the fitted values are positive. The error distribution appropriate to the counts is Poisson. Where one categorical variable is considered as a dependent variable and the other(s) as independent, then the log-linear analysis is a LOGISTIC REGRESSION, and it has a LOGIT LINK.
MARGINALITY. Marginality concerns the relationship between interactions and main effects in GLM. The main effects A and B are said to be marginal to their interaction A*B. Similarly, A*B is said to be marginal to any higher order interaction containing it such as A*B*C. There are three main considerations of marginality: (i) A model formula must be hierarchical, i.e. it should not contain an interaction term unless it also contains all the main effects involved, which must precede it in the model formula. (ii) If an interaction is accepted to be important, then the corresponding main effects should be regarded as important without regard to their significance levels. (iii) A main effect should not be tested using a sum of squares that has been adjusted for an interaction involving the main effect.
MARKOV CHAINS. Imagine a sequence of trials and a discrete sample space for each trial consisting of a finite number of sample points. Assume that the probability of an outcome in any trial depends upon the outcome of the trial immediately preceding it. Thus there are transition probabilities, pij, which represent the probabilities of outcome Ej in any particular trial, given that outcome Ei occurred in the preceding trial. The outcomes E1 ... En are called states. Probabilities of outcomes can then be calculated for a whole series of trials, given information on the probability ak of outcome Ek in the initial trial. This kind of process is called a Markov chain, and the transition probabilities pij are commonly presented in matrix form. Each row of such a matrix is a probability vector, because it has non-negative components which sum to 1. An example of a problem employing a two-state Markov chain would be to describe the sequence of wet and dry days at a particular location. The probability that tomorrow will be dry, given the preceding sequence of wet and dry days, is assumed to depend only on whether today is wet or dry. A more general model could allow for higher-order dependence in the sequence of wet and dry days, a continuous component for the amount of rain on wet days and seasonal variation in the parameters which govern the behaviour of the model.
MARKOVIAN TRANSITIONS. The probability of moving between two strata depending on the stratum in which one is at time t. A Non-markovian transition (Markovian chain of order 2) is the probability of moving between two strata that is dependent on the stratum occupied at any time prior to time t.
MAXIMUM LIKELIHOOD ESTIMATORS. For data with normal errors and an identity link, least squares estimators in linear regression and anova are also the maximum likelihood estimators. For other kinds of error and different link functions, however, the methods of least squares do not give unbiased parameter estimates, and maximum likelihood methods are preferred. Maximum likelihood estimators are the values of the parameters which correspond to the maximum value of the LIKELIHOOD FUNCTION, or equivalently, to the maximum of the logarithm of the likelihood function. Given the data, and a specific model embodying the best available hypothesis about the factors involved, the objective is to find the values of the parameters that maximise the likelihood of the data being observed.
MEAN SQUARE. (MS). The mean square is the sum of squares divided by the degrees of freedom. The F-ratio is the ratio of TREATMENT to ERROR mean squares.
MODEL FORMULA. A statement of the hypothesised relationship between VARIABLES,
to be tested in a general linear model. The left-hand side of the equation
takes the dependent variables (continuous, except in LOG-LINEAR models), and
the right-hand side takes the independent variables (categorical in ANOVA,
continuous in REGRESSION). For example, model Y = A|B
tests the relationship of Y to the two dependent variables A and
B, and to their interaction A*B. The model Y =
X for continuous Y and X tests for a significant linear
regression of the form Y = b0 +
b1X + error{~N(0, 2)}. For
all models, a non-significant result indicates that the only model supported by
the data is the simplest one, namely Y = constant.
2)}. For
all models, a non-significant result indicates that the only model supported by
the data is the simplest one, namely Y = constant.
MODEL SELECTION. The preferred approach is to begin with a fully parametised model that fits the data and to decrease the dimensionality toward a more parsimonious model that is supported by the data (step-down methods). Thus, in ANOVA, we ask firstly whether the highest order interaction can be eliminated without significantly degrading the fit of the model to the data, then lower orders, and so on. The alternative is to start with a simple model and increase the dimensionality, but misleading tests may be produced if the first model does not fit the data.
MULTINOMIAL DISTRIBUTION. A discrete probability distribution in which an attribute can have more than two classes (the BINOMIAL DISTRIBUTION is a special case of it). The G-test is based on this distribution. The probability of observing cell frequencies a, b, c, d, assuming a multinomial distribution is:
(a/n)a(b/n)b(c/n)c(d/n)d n! / (a!b!c!d!)
MULTIVARIATE ANALYSIS OF VARIANCE. (MANOVA). A technique for evaluating differences among centroids (average on the combined variables) for a set of dependent variables when there are two or more levels of an independent variable (one-way manova). Factorial manova is the extension to designs with more than one independent variable. Once a significant relationship is established, techniques are available to assess which dependent variables are influenced by the independent variable. The method makes many assumptions, including multivariate normality, homogeneity of variance-covariance matrices, and linearity among all pairs of dependent variables. Severe problems can be caused by unequal sample sizes, missing data, outliers, and multicollinearity of dependent variables. MANOVA is a special case of CANONICAL ANALYSIS.
NEGATIVE BINOMIAL DISTRIBUTION. Many contagious populations of categorical
data can adequately be expressed by the negative binomial: described by the
mean and exponent k, with k in the region of 2. Larger values of
k approach the Poisson distribution at k = 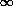 , whilst fractional
values of k indicate a distribution tending towards the logarithmic
series (another contagious model) at k=0. The formula for the
negative binomial distribution is:
, whilst fractional
values of k indicate a distribution tending towards the logarithmic
series (another contagious model) at k=0. The formula for the
negative binomial distribution is:
P(y) = [k/(µ+k)]k [µ/(µ+k)]y (k+y-1)! / [y!(k-1)!]
NONPARAMETRIC TECHNIQUES. (distribution-free methods). These statistical procedures are not dependent on a given underlying distribution of responses in the population from which the sample is drawn, but only on the distribution of the variates themselves. Another linked property is scale invariance: applying a transformation to the data does not affect the result. They are mostly based on the idea of ranking the variates after pooling all groups and considering them as a single sample for the purposes of ranking. See Con p. 91-93 for comments on the definition of nonparametric statistics. In cases where the parametric assumptions hold entirely or even approximately, the parametric test is generally the more efficient statistical procedure for detecting departures from the null hypothesis. Parametric tests are also generally more flexible, capable for example of dealing with a mixture of categorical and continuous variables, which is not possible with non-parametric tests.
NORMAL PROBABILITY DISTRIBUTION. Describes a frequency distribution of a
continuous variable which is symmetrical about the mean, so mean median and
mode are all at the same point. For continuous variables, the theoretical
probability distribution, or normal probability density function, can be
represented by the expression Z =
e-(Y-µ)2 / (2 2) / [
2) / [
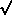 (2
(2 )]. The value of
Z indicates the height of the ordinate of a continuous curve, and it
represents the density of the items (density means the relative concentration
of variates at a distance of Y from µ). A normal probability
density function thus has two parameters: the parametric mean (µ) and
the parametric standard deviation (
)]. The value of
Z indicates the height of the ordinate of a continuous curve, and it
represents the density of the items (density means the relative concentration
of variates at a distance of Y from µ). A normal probability
density function thus has two parameters: the parametric mean (µ) and
the parametric standard deviation ( ) which determine
respectively the location and the shape of the distribution. Probability
density functions are defined so that the expected frequency of observations
between two class limits is represented by the area between these limits under
the curve. A normal frequency distribution extends from -
) which determine
respectively the location and the shape of the distribution. Probability
density functions are defined so that the expected frequency of observations
between two class limits is represented by the area between these limits under
the curve. A normal frequency distribution extends from -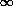 to +
to +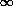 along the axis
of the variable, although 95.46% of values are within two parametric standard
deviations of the mean and 99.72% are within three parametric standard
deviations (95% within 1.96
along the axis
of the variable, although 95.46% of values are within two parametric standard
deviations of the mean and 99.72% are within three parametric standard
deviations (95% within 1.96 ). Both the binomial distribution:
(p+q)k and the multinomial distribution:
(p+q+r+...+z)k approach the
normal frequency distribution as k approaches infinity. From the density
function for Z, we could generate a normally distributed sample using
random numbers, which might represent, for example, distances from a source
achieved by n particles moving in either direction along a straight
line. We must first define the shape we desire for our density function, by
specifying an average value for the squared distances of particles from the
origin: the VARIANCE. This could be larger, for a more flattened bell shape, or
smaller for a taller bell with narrower tails. We then simply allow for each
independent value of distance, Yi (the random number)
separating the particle from its origin, to be obtained with a probability that
is a function of this variance,
). Both the binomial distribution:
(p+q)k and the multinomial distribution:
(p+q+r+...+z)k approach the
normal frequency distribution as k approaches infinity. From the density
function for Z, we could generate a normally distributed sample using
random numbers, which might represent, for example, distances from a source
achieved by n particles moving in either direction along a straight
line. We must first define the shape we desire for our density function, by
specifying an average value for the squared distances of particles from the
origin: the VARIANCE. This could be larger, for a more flattened bell shape, or
smaller for a taller bell with narrower tails. We then simply allow for each
independent value of distance, Yi (the random number)
separating the particle from its origin, to be obtained with a probability that
is a function of this variance,  2.
Specifically, Z(Yi) = f {1/(
2.
Specifically, Z(Yi) = f {1/( eYi2/
eYi2/ 2 )}, so
distances from the origin many times larger than the average squared distances
(
2 )}, so
distances from the origin many times larger than the average squared distances
( 2) are very rare[1]. For variables commonly encountered in
nature, there is a strong tendency for the measurements of individuals in
different populations all to exhibit this same normal distribution. More
generally, whatever the distribution of measurements, the distribution of
sample means tends to become normal under random sampling as the sample size
increases (CENTRAL LIMIT THEOREM). Natural situations that could give rise to a
normal distribution are those in which myriad independent forces in nature,
themselves subject to variation, combine additively to produce a central
tendency. The variable might be the volume of a water droplet in a cloud, or
the height of a barley stem in a field. By taking repeated independent measures
of volume (or height), we obtain a sample distribution of values. We can apply
the central limit theorem to obtain CONFIDENCE LIMITS to this sample mean
(whether or not it is normally distributed) as an estimate of the population
mean µ, based on the average of the squared deviations (VARIANCE).
Further analysis of this variance (ANOVA) allows us to compare mean responses
under different levels of a treatment (seeding technique, say), to test whether
the part of the variance explained by the treatment effect is any greater than
the residual (unexplained) variance. As this kind of technique makes inferences
with respect to normally distributed residuals, the response variable may
require prior TRANSFORMATION. The normal distribution is thus a useful tool for
describing the attributes of a continuous variable and analysing the various
influences on its location in sample space. It is the most widely used
distribution in statistics, having three main applications: (i) numerous
parametric tests are based on the assumption of normally distributed errors;
(ii) knowing whether a sample is or is not normally distributed may
confirm or reject certain underlying hypotheses (causal factors affecting the
variable are or are not additive, independent and of equal variance);
(iii) assuming normality allows us to make predictions and tests of
given hypotheses based upon this assumption (e.g. the chance of obtaining a
variable x standard deviation units away from the mean). For an event
that is counted into categories (as opposed to a variable measured along a
continuum), the appropriate probability distribution for analysing the
contingency table is the POISSON.
2) are very rare[1]. For variables commonly encountered in
nature, there is a strong tendency for the measurements of individuals in
different populations all to exhibit this same normal distribution. More
generally, whatever the distribution of measurements, the distribution of
sample means tends to become normal under random sampling as the sample size
increases (CENTRAL LIMIT THEOREM). Natural situations that could give rise to a
normal distribution are those in which myriad independent forces in nature,
themselves subject to variation, combine additively to produce a central
tendency. The variable might be the volume of a water droplet in a cloud, or
the height of a barley stem in a field. By taking repeated independent measures
of volume (or height), we obtain a sample distribution of values. We can apply
the central limit theorem to obtain CONFIDENCE LIMITS to this sample mean
(whether or not it is normally distributed) as an estimate of the population
mean µ, based on the average of the squared deviations (VARIANCE).
Further analysis of this variance (ANOVA) allows us to compare mean responses
under different levels of a treatment (seeding technique, say), to test whether
the part of the variance explained by the treatment effect is any greater than
the residual (unexplained) variance. As this kind of technique makes inferences
with respect to normally distributed residuals, the response variable may
require prior TRANSFORMATION. The normal distribution is thus a useful tool for
describing the attributes of a continuous variable and analysing the various
influences on its location in sample space. It is the most widely used
distribution in statistics, having three main applications: (i) numerous
parametric tests are based on the assumption of normally distributed errors;
(ii) knowing whether a sample is or is not normally distributed may
confirm or reject certain underlying hypotheses (causal factors affecting the
variable are or are not additive, independent and of equal variance);
(iii) assuming normality allows us to make predictions and tests of
given hypotheses based upon this assumption (e.g. the chance of obtaining a
variable x standard deviation units away from the mean). For an event
that is counted into categories (as opposed to a variable measured along a
continuum), the appropriate probability distribution for analysing the
contingency table is the POISSON.
ODDS RATIO. Given by 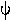 =
[
=
[ 1/(1-
1/(1- 1)] /
[
1)] /
[ 2/(1-
2/(1- 2)]. This is the ratio of
relative likelihood (the odds) of failure (
2)]. This is the ratio of
relative likelihood (the odds) of failure ( ) between
two groups, one exposed to a condition (treatment) and the other not exposed
(placebo). Test H0:
) between
two groups, one exposed to a condition (treatment) and the other not exposed
(placebo). Test H0: 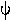 = 1 and obtain confidence intervals for
= 1 and obtain confidence intervals for 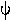 from the RISK RATIO, which is the ratio of rates of failure. The
logarithm of the odds ratio is called the LOGIT FUNCTION, which is the link
function used for analysing proportional data with LOGISTIC REGRESSION.
Logistic regression can therefore be used to obtain odds for the hypothesis
that the likelihood of failure, or occurrence, is dependent on the treatment
(which can have more than two levels, or be continuous).
from the RISK RATIO, which is the ratio of rates of failure. The
logarithm of the odds ratio is called the LOGIT FUNCTION, which is the link
function used for analysing proportional data with LOGISTIC REGRESSION.
Logistic regression can therefore be used to obtain odds for the hypothesis
that the likelihood of failure, or occurrence, is dependent on the treatment
(which can have more than two levels, or be continuous).
ORTHOGONALITY. Two variables are orthogonal if knowledge of one gives no clue as to the value of another. In a factorial GLM with, say, two treatments and three levels of each treatment, the two main effects are orthogonal if the same number of observations are made for all of the level combinations. The adjusted sums of squares (adjusted for all other variables in the analysis) are then identical to the sequential sums of squares (adjusted only for lower order variables). Orthogonality of all pairs of factors thus allows inferences to be drawn separately about the different factors, greatly simplifying interpretation of results. Examples of non-orthogonal designs might be (i) WEIGHT = LLEG + RLEG, where the two main effects are left and right leg length (although each is highly significant on its own, neither effect is significant when adjusted for the other, because they are correlated, so not all level combinations are represented); (ii) AGE = BIRTHDATE + DEATHDATE (each main effect on its own is very uninformative about age, yet both adjusted effects are significant).
PARAMETERS. The true mean, µ, and error variance,
 2, of a variable are the unknown constants, termed
parameters, which are a permanent and underlying feature of a population,
compared to the parameter estimates which are derived from the sample of
measurements. Other examples of parameters might be survival rate,
2, of a variable are the unknown constants, termed
parameters, which are a permanent and underlying feature of a population,
compared to the parameter estimates which are derived from the sample of
measurements. Other examples of parameters might be survival rate,
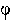 i, and capture rate, pi in
capture-mark-recapture studies. An ANOVA model has one parameter for each level
of each variable, so the number of parameters in model Y =
A|B|C is a*b*c.
i, and capture rate, pi in
capture-mark-recapture studies. An ANOVA model has one parameter for each level
of each variable, so the number of parameters in model Y =
A|B|C is a*b*c.
PARSIMONY, LAW OF (OCCAM'S RAZOR). No more causes should be assumed than will account for the effect. A simpler model which describes the data may be preferable to a more complicated one which leaves little of the variability 'unexplained' but has fewer degrees of freedom and therefore less statistical power to reject the null hypothesis when it should be rejected.
PERMUTATIONS. The number of permutations that can be formed of n items taken r at a time (no repetitions, order important): nPr = n! / (n-r)! If repetition is allowed, then the number of ordered samples is nr.
POISSON DISTRIBUTION. A discrete probability distribution of the number of
times a rare event occurs. In contrast to the BINOMIAL, the number of times
that an event does not occur is infinitely large. If the mean number of
occurrences is 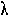 , then the probability of observing x
occurrences is given by: e-
, then the probability of observing x
occurrences is given by: e-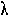
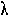 x /
x! The purpose of fitting a Poisson distribution to numbers of rare
events in nature is to test that there is an equal probability of an organism
occupying any point in space and that the presence of one individual does not
influence the distribution of another i.e. that the events occur independently
with respect to each other. If they do, they will follow the Poisson
distribution. If the occurrence of one event impedes that of a second such
event in the sampling unit, we obtain a repulsed, spatially or temporally
uniform distribution. If the occurrence of one event enhances the probability
of a second such event, we obtain a clumped or contagious distribution (see
NEGATIVE BINOMIAL DISTRIBUTION). The Poisson distribution can be used as a test
for randomness or independence of distribution not only spatially but also in
time. The curve of the Poisson series is described completely by one parameter,
as the variance is equal to the mean. A rapid test of whether an observed
frequency distribution is distributed in Poisson fashion is given by the
coefficient of dispersion: CD = (SD2)/mean. This value will
be near 1 in distributions that are essentially Poisson, will be > 1 in
clumped samples, and < 1 in cases of repulsion.
x /
x! The purpose of fitting a Poisson distribution to numbers of rare
events in nature is to test that there is an equal probability of an organism
occupying any point in space and that the presence of one individual does not
influence the distribution of another i.e. that the events occur independently
with respect to each other. If they do, they will follow the Poisson
distribution. If the occurrence of one event impedes that of a second such
event in the sampling unit, we obtain a repulsed, spatially or temporally
uniform distribution. If the occurrence of one event enhances the probability
of a second such event, we obtain a clumped or contagious distribution (see
NEGATIVE BINOMIAL DISTRIBUTION). The Poisson distribution can be used as a test
for randomness or independence of distribution not only spatially but also in
time. The curve of the Poisson series is described completely by one parameter,
as the variance is equal to the mean. A rapid test of whether an observed
frequency distribution is distributed in Poisson fashion is given by the
coefficient of dispersion: CD = (SD2)/mean. This value will
be near 1 in distributions that are essentially Poisson, will be > 1 in
clumped samples, and < 1 in cases of repulsion.
PROBABILITY DENSITY FUNCTION. Discrete sample spaces describe sample points
that can be counted off as integers, but continuous sample spaces describe
continuous variables, such as the position of a particle moving along a
straight line, or any response variable in a GLIM. Probabilities in continuous
sample space can be defined in terms of the distribution function, F(x),
which is the probability that the sample point has any value < a
specified value x. This takes a sigmoid form between zero probability at
x = -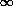 and 1 at x = +
and 1 at x = +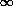 . The derivative of F(x) is the
probability density function f(x) which is a bell-shaped curve. The
probability of x lying between two limits a and b is given
by the area under this curve between x = a and x =
b, i.e. the integral of f(x) with respect to x between
limits a and b.
. The derivative of F(x) is the
probability density function f(x) which is a bell-shaped curve. The
probability of x lying between two limits a and b is given
by the area under this curve between x = a and x =
b, i.e. the integral of f(x) with respect to x between
limits a and b.
PSEUDOREPLICATION. In analysis of variance pseudoreplication occurs when treatment effects are measured against an error term that has more degrees of freedom than are appropriate for the hypothesis being tested. A valid F-ratio is one in which the denominator contains all of the components of variance that are in the numerator except the one component of variance that is being tested. See Methods: Analysis of variance for correct choice of error terms in nested designs.
RANDOM EFFECTS. A level within a treatment is considered as a random effect if it is not exactly repeatable, and if it represents a random sample from the population about which it is desired to draw conclusions. Subjects are generally treated as random effects (written S' in model description). A random effect other than subject acts like an extra error term in the model and considerably complicates hypothesis testing. See also FIXED EFFECTS.
RANDOMISATION. A technique for testing the chance of type I error under the null hypothesis by repeated random assignment of the data to treatment levels. R.A. Fisher claimed that statistical conclusions have no justification beyond the fact that they agree with those which could have been arrived at by this elementary method. Randomisation tests are useful with standard test statistics (e.g. t, F) applied to non-normal data: a P-value is obtained from repeated recalculation of the statistic with a response variable that is randomised between all treatment levels, and comparison with the original observed statistic. Randomisation is one of the RESAMPLING METHODS (see Methods section).
REGRESSION. Regression equations of the form Y = b0 +
b1X + error{~N(0, 2)} are
employed (i) in order to lend support to hypothesis regarding the
possible causation of changes in Y by changes in X; (ii)
for purposes of prediction, of Y in terms of X; and (iii)
for purposes of explaining some of the variation of Y by X, by
using the latter variable as a statistical control. The least squares linear
regression line through a set of points in two dimensions is defined as the
straight line that results in the sum of squared residuals being minimised
(i.e. the COEFFICIENT OF DETERMINATION being maximised). This line must pass
through
2)} are
employed (i) in order to lend support to hypothesis regarding the
possible causation of changes in Y by changes in X; (ii)
for purposes of prediction, of Y in terms of X; and (iii)
for purposes of explaining some of the variation of Y by X, by
using the latter variable as a statistical control. The least squares linear
regression line through a set of points in two dimensions is defined as the
straight line that results in the sum of squared residuals being minimised
(i.e. the COEFFICIENT OF DETERMINATION being maximised). This line must pass
through 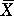 ,
, 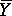 . The analysis is equivalent to a one-way ANOVA, and tests
the slope for a significant deviation from zero. The slope can also be tested
against zero using t = b1/SEb1. In
multiple regression, the several independent variables are combined into
a predicted value to produce, across all subjects, the highest correlation
between the predicted value and the response variable. A multiple regression
with two continuous independent variables produces a plane; a significant
INTERACTION effect is indicated by the slope of the plane in
X1 being different to the slope in X2. A
multiple regression with one continuous and one categorical independent
variable (an ANCOVA design) produces one line for each level of the categorical
variable (could be ordinal treated as categorical); a significant interaction
effect is indicated by differences in the slopes of the lines. All forms of
regression, including higher orders, can be analysed in GLM. A regression of
the form Y = X + XX is a polynomial, for which
considerations of MARGINALITY apply. Analyses of regression make all the
ASSUMPTIONS of parametric analysis of variance. Non-linear relationships can be
analysed after TRANSFORMATION. Model I regression assumes the independent
variable X is measured without error, so the X variable is a
FIXED EFFECT and the residuals are measured in Y only (vertical
distances to the regression line). It estimates a relationship with one
variable-as-measured and the best prediction of the other. Model II regression
is less frequently used; it assumes that both Y and X are
measured with error, and it gives a regression line lying between the Y
on X and the X on Y regressions. The model II regression
estimates a slope between two variables that are meaningful only when
measurement error is the sole cause of statistical error, otherwise the
variables are virtually meaningless.
. The analysis is equivalent to a one-way ANOVA, and tests
the slope for a significant deviation from zero. The slope can also be tested
against zero using t = b1/SEb1. In
multiple regression, the several independent variables are combined into
a predicted value to produce, across all subjects, the highest correlation
between the predicted value and the response variable. A multiple regression
with two continuous independent variables produces a plane; a significant
INTERACTION effect is indicated by the slope of the plane in
X1 being different to the slope in X2. A
multiple regression with one continuous and one categorical independent
variable (an ANCOVA design) produces one line for each level of the categorical
variable (could be ordinal treated as categorical); a significant interaction
effect is indicated by differences in the slopes of the lines. All forms of
regression, including higher orders, can be analysed in GLM. A regression of
the form Y = X + XX is a polynomial, for which
considerations of MARGINALITY apply. Analyses of regression make all the
ASSUMPTIONS of parametric analysis of variance. Non-linear relationships can be
analysed after TRANSFORMATION. Model I regression assumes the independent
variable X is measured without error, so the X variable is a
FIXED EFFECT and the residuals are measured in Y only (vertical
distances to the regression line). It estimates a relationship with one
variable-as-measured and the best prediction of the other. Model II regression
is less frequently used; it assumes that both Y and X are
measured with error, and it gives a regression line lying between the Y
on X and the X on Y regressions. The model II regression
estimates a slope between two variables that are meaningful only when
measurement error is the sole cause of statistical error, otherwise the
variables are virtually meaningless.
REPEATED MEASURES. Refers to an experimental design for ANOVA or GLM in which the subjects are measured more than once and where all measurements are to be included in the analysis. There are two reasons for doing this: (i) when interested in the effects of time (e.g. before and after a treatment), (ii) in a cross-over design in which each subject receives more than one treatment (in different orders). Otherwise, take a single mean for each subject and use the means as independent variates in the analysis. In order to account for repeated measures in analysis of variance, either add another treatment to the experiment called individual, or use a split-plot design with subjects nested in at least one of the treatments while being cross-factored with at least one treatment (mixed design). In the latter case, care must be taken to use the proper error mean squares in calculating F-ratios for the main effects and interactions (to avoid PSEUDOREPLICATION).
REPLICATION. Statistical knowledge is only achieved through replication. In
analysis of variance, replicate observations are required at each treatment
level in order to obtain a base-line estimate of variation within levels, from
which to distinguish variation between levels. A treatment mean is estimated
with standard error of  /n, so a larger n reduces
the standard error, and also provides a more precise estimate of
/n, so a larger n reduces
the standard error, and also provides a more precise estimate of
 .
.
RESAMPLING METHODS. Methods that involve taking samples from the original data set (randomisation, bootstrap, jackknife) or from a stochastic process like the one believed to have generated the data set (Monte Carlo). See Crowley, P.H. (1992) Annu. Rev. Ecol. Syst. 23:405-47.
RESIDUAL. The amount by which the observed value differs from the value predicted by the model. Also called errors, residuals are the segments of scores not accounted for by the analysis.
RISK RATIO. The ratio of two rates of failure: 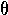 =
=
 1/
1/  2. The point estimate of
2. The point estimate of
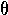 is given by p1 / p2 =
(X/n1) / (Y/n2), where
X/n1 is the rate for the treatment sample (exposed to
a condition), and Y/n2 is the rate for the placebo
(not exposed), both of which have binomial distributions:
B(n1,
is given by p1 / p2 =
(X/n1) / (Y/n2), where
X/n1 is the rate for the treatment sample (exposed to
a condition), and Y/n2 is the rate for the placebo
(not exposed), both of which have binomial distributions:
B(n1,  1) and B(n2,
1) and B(n2,
 2) respectively. For H0:
2) respectively. For H0:
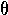 = 1, the significance of the difference between the rates can
be tested with a chi-squared test or a Z-test on the 2x2 contingency table of
occurrences (
= 1, the significance of the difference between the rates can
be tested with a chi-squared test or a Z-test on the 2x2 contingency table of
occurrences (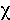 2 = Z 2). When the proportions
are not too small (n
2 = Z 2). When the proportions
are not too small (n and n(1-
and n(1- ) both > 5)
and the sample sizes are large, then approximate normality can be assumed in
calculating confidence intervals for the point estimate of
) both > 5)
and the sample sizes are large, then approximate normality can be assumed in
calculating confidence intervals for the point estimate of 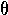 .
Thus, the new variable W = p1 -
.
Thus, the new variable W = p1 -
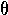 p2 has a mean of zero and an approximately normal
distribution, which is given by Fieller's theorem as:
p2 has a mean of zero and an approximately normal
distribution, which is given by Fieller's theorem as:
N( 1-
1- 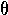
 2,
2,
 1(1-
1(1- 1)/n1 +
1)/n1 +
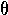 2
2 2(1-
2(1- 2)/n2) ~ N(0,
2)/n2) ~ N(0,  2).
2).
The population parameters are replaced by sample
values in order to estimate  , and hence confidence limits for the estimated
, and hence confidence limits for the estimated
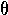 , at ± 1.96
, at ± 1.96 /p2. See D. Katz et al.
(1978) Biometrics 34:469, Method B. Because ratios are not in fact
symmetric (values all > 0), this estimate can be improved on by using the
log of the observed ratio (Method C). A generalisation of this method, suitable
for small sample sizes, is proposed by B.J.R. Bailey (1987) Biometrics
43:201. The value of Z from the 2x2 contingency table then corresponds
to one of these confidence intervals approximating unity. See also the ODDS
RATIO, which considers the odds of failure to success, and is suitable
for testing with LOGISTIC REGRESSION.
/p2. See D. Katz et al.
(1978) Biometrics 34:469, Method B. Because ratios are not in fact
symmetric (values all > 0), this estimate can be improved on by using the
log of the observed ratio (Method C). A generalisation of this method, suitable
for small sample sizes, is proposed by B.J.R. Bailey (1987) Biometrics
43:201. The value of Z from the 2x2 contingency table then corresponds
to one of these confidence intervals approximating unity. See also the ODDS
RATIO, which considers the odds of failure to success, and is suitable
for testing with LOGISTIC REGRESSION.
ROBUST. A robust statistic is one that correctly rejects the null hypothesis at
a given 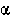 level the right number of times even if the distributions do
not meet the assumptions of the analysis.
level the right number of times even if the distributions do
not meet the assumptions of the analysis.
SAMPLE. A collection of individual observations selected by a specified procedure. In most cases the sample size is given by the number of subjects.
SAMPLING DISTRIBUTION. A distribution of statistics (not raw scores) computed from random samples of a given size taken repeatedly from a population. For example, in one-way ANOVA, hypotheses are tested with respect to the sampling distribution of means.
STANDARD DEVIATION. The classical and most widely used measure of dispersion. The standard deviation is a combined measure of the distances of observations from their mean, given by the square-root of the VARIANCE.
STANDARD ERROR OF THE MEAN. Refers to the standard deviation of the means of
random samples of n measurements from any population (not necessarily
normal) with mean µ and standard deviation  . The
frequency distribution of the sample meansY in these repeated samples
approaches a normal distribution as n increases, with mean µ and
standard deviation
. The
frequency distribution of the sample meansY in these repeated samples
approaches a normal distribution as n increases, with mean µ and
standard deviation  /
/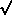 n. This standard error is used
to describe the reliability of a sample mean in indicating the population mean,
in the same way that the standard deviation is used to describe the reliability
of a single random measurement in doing so, assuming normality. Note that
larger sample sizes yield estimates of means less variable than those based on
few items. Generally, we only have a single sample and a sample estimate s
of the parametric standard deviation
n. This standard error is used
to describe the reliability of a sample mean in indicating the population mean,
in the same way that the standard deviation is used to describe the reliability
of a single random measurement in doing so, assuming normality. Note that
larger sample sizes yield estimates of means less variable than those based on
few items. Generally, we only have a single sample and a sample estimate s
of the parametric standard deviation  . Having computed the
sample mean, however, we can state that this is our best estimate of the true
mean (µ) and attach standard errors to it: SE = s
/
. Having computed the
sample mean, however, we can state that this is our best estimate of the true
mean (µ) and attach standard errors to it: SE = s
/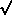 n. This is the estimate of the standard deviation of means we
would expect were we to obtain a collection of means based on equal-sized
samples of n items from the same population. This standard error can
then be used to compute CONFIDENCE LIMITS for the population mean.
n. This is the estimate of the standard deviation of means we
would expect were we to obtain a collection of means based on equal-sized
samples of n items from the same population. This standard error can
then be used to compute CONFIDENCE LIMITS for the population mean.
STATISTICAL POWER. The ability of a statistical test to reject the null hypothesis when it should be rejected. Tests with few degrees of freedom have low power.
SUM OF SQUARES. The sum of squared deviations from the mean, given by:
 (Y -
(Y - 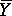 ) 2 =
) 2 =  Y 2 - (
Y 2 - ( Y
)2 / n
Y
)2 / n
The average of these squared deviations is the VARIANCE. From top to bottom of an analysis of variance table, the sequential sums of squares reveal the improvement in prediction provided by each variable when added to the variables above it in the table. These sums of squares add up to the total sums of squares. The adjusted (unique) sum of squares for a variable measures the improvement in prediction when all the other variables in the table are assumed already known. See MARGINALITY for appropriate interpretation of sums of squares.
TAILS. One-tailed or two-tailed tests refers to whether the region of rejection for H0 corresponds to one or both tails of the test statistic. A test is two-tailed when H0 alone is tested, and one-tailed when H0 is tested against an alternative, H1, specifying direction. If a t-test is used to express the significance of a correlation coefficient it is one-tailed when the question is whether a positive (or whether a negative) relationship is significant, and two-tailed (less commonly) when unspecified interdependency is being tested. With observed sex ratios, if the question is whether females appear more often than males the appropriate test is one-tailed; if the question is simply whether the sexes are unequal in frequency, i.e. in the absence of any preconception about the direction of departures from expectation, the test is two-tailed.
TRANSFORMATIONS. Used to meet the assumptions of parametric tests. In a GLM, transform continuous variables X and/or Y to obtain linearity; transform Y to obtain homogeneity of variances and normality of errors. Data that are known to be non-normal (such as proportions) should be transformed by default, whether or not the data are sufficient to demonstrate non-normality. Normality is usually tested from the residuals of all samples combined. Transformations have increasing strength from square-root (for counts) to log (for mean positively correlated with variance) to inverse. The arcsine transformation is appropriate to proportions.
TREATMENTS. The experimental manipulations against which the response variable is being tested. Treatments are the categorical explanatory variables on the right hand side of the MODEL FORMULA. A one-way ANOVA has one treatment with a levels or samples (tested against Fa-1,n-a); a two-way anova has two treatments, and so on. Cross factored treatments describes the case where all level combinations of two or more treatments are tested. Nested treatments describes the case where all the levels of one treatment do not receive all the levels of a second treatment. The error term of any anova contains subjects nested in one or more of the treatments, but treatments can also be nested in each other (e.g. supervisors nested in university for analysis of tutee performance).
TYPES OF ERROR. Before carrying out a test we have to decide what magnitude of
type I error (rejection of a true null hypothesis) we are going to allow.
Chance deviation of some samples are likely to mislead us into believing our
hypothesis H0 to be untrue. Type I error is expressed as a
probability symbolised by 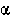 (when expressed as a percentage it is known
as significance level). Evaluating the probability of type II error (acceptance
of a false null hypothesis) is problematic because if H0 is
false, some other hypothesis H1 must be true and this must be
specified before type II error can be calculated.
(when expressed as a percentage it is known
as significance level). Evaluating the probability of type II error (acceptance
of a false null hypothesis) is problematic because if H0 is
false, some other hypothesis H1 must be true and this must be
specified before type II error can be calculated.
VARIABLE. A property that varies in a measurable way between subjects in a sample. The Response, outcome or dependent variable (Y) describes the measurements, usually on a continuous scale, regarded as random variables. These measurements are free to vary in response to the independent, explanatory or predictor variables (X) which are treated as though they are non-random measurements or observations (e.g. fixed by experimental design). In GLIM, these variables in the model are called vectors. Measurements are made on nominal, ordinal (rank), or continuous (interval and ratio) scales. Nominal and ordinal data are usually recorded as the numbers of observations in each category, in which case the counts are called discrete variables. A qualitative, (categorical) explanatory variable is called a factor or treatment and its categories are called the levels of the factor. An ANOVA approach is usually adopted for designs with one or more categorical independent variables. A quantitative explanatory variable is called a covariate or effect. A REGRESSION approach is usually adopted for analysis of one or more covariates. In situations with both qualitative and quantitative explanatory variables, two alternative procedures can be adopted: ANCOVA, or regression with dummy variables. Statistical techniques for analysing categorical response variables, such as LOG-LINEAR models assume that the data result from the cross-classification of separate items. For true categorical response variables, statistical techniques can assume that the number in each cell of a contingency table has a Poisson Distribution. Because this in turn implies that the variance is equal to the mean, then there is no need to estimate an error mean square because the size of the error is specified by the mean.
VARIANCE. Describes the average of n squared deviations from the mean.
Its positive root,  , is one parameter in the NORMAL
DISTRIBUTION, the other being the mean, µ. A sample variance,
s2, is an unbiased estimate of the population variance,
, is one parameter in the NORMAL
DISTRIBUTION, the other being the mean, µ. A sample variance,
s2, is an unbiased estimate of the population variance,
 2, when the sum of squares is divided by
n-1. The variance can be calculated without reference to the mean, using
the formula:
2, when the sum of squares is divided by
n-1. The variance can be calculated without reference to the mean, using
the formula:
s2 = [  Y 2 - (
Y 2 - ( Y )2 /
n ] / (n - 1)
Y )2 /
n ] / (n - 1)
The component in square brackets is the SUM OF SQUARES, equivalent to
 (Y -
(Y - 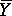 )2.
)2.
VARIANCE. COVARIANCE MATRIX. This is a square and symmetrical matrix, with the variances of each variable in the main diagonal, and the covariances between different variables in the off-diagonal elements.
VARIATE. Refers to a single reading Yi, score or observation of a given response variable Y.
ANALYSIS OF VARIANCE. (>1 sample)
1. Parametric
Assumes sampling at random (S&R p. 401), linearity for continuous effects, normally distributed error terms (chi-squared and Kolmogorov-Smirnov tests, S&R p. 412), independence of variates (S&R p. 401), homogeneity of variances (Fmax test or Bartlett's test, S&R p. 402), additivity (two-way anova, S&R p. 414). Data may sometimes be transformed to meet the assumptions (S&R p. 417).
a) One-way analysis of variance
i) Single classification anova for the general case of a samples (levels) from a single variable (treatment) A and ni variates (subjects) per sample (S&R p. 210). H0: the a samples come from populations having the same distribution. The full model is Y = A + error{S'(A)}. Significance is tested with F = MS[treatment] / MS[error] at a-1 and n-a degrees of freedom for a levels (samples) of the treatment and n subjects. Is n big enough for the test (S&R p. 262)? Post hoc comparisons of treatment levels can reveal where significance lies. See Day, R.W. & Quinn, G.P. (1989) Ecol. Monog. 59:433-463. For example, Student-Newman-Keuls procedure (S&R p. 262) or Welsch step-up procedure (S&R p. 253) test all differences between pairs of means.
ii) t-test of the difference between two means is mathematically equivalent to the anova (ts2 = Fs). When variances are not equal in small samples (ns < 30) use Mann-Whitney U-test or approximate t (S&R p. 411; Par p. 21).
iii) Single observation compared with a sample (S&R p. 231).
b)
i) Factorial analysis of variance for orthogonal designs, without replication in treatment combinations (assumes additivity of factors), or with replication (interactions can be tested). The full model for two cross-factored treatments is Y = X1 + X2 + X1X2 + error {S'(X1X2)}. The two main effects (with a1-1 and a2-1 d.f.) and the interaction ([a1-1].[a2-1] d.f.) are tested against the error term, of subjects nested in X1 and X2 (n-a1a2 d.f.).
ii) Nested analysis of variance. For example, subjects nested in A nested in B. The full model takes the form: Y = B + A'(B) + S'[A(B)]. The two treatments are not cross-factored so there is no interaction term. Treatment B is tested with A'(B) error MS; A'(B) is tested with S'[A(B)] error MS.
iii) Repeated measures analysis of variance. The full model takes the form: Y = S' + X + error {S'X}. A t-test for paired comparisons is equivalent to this design with just two levels of X (e.g. before and after), and is a special case of randomised complete blocks. Where there are more repeated measures per subject than subjects, then it is recommended to do one model per subject.
iv) Split plot, or mixed, design (repeated measures). For example, subjects nested in treatment (A), and cross-factored with time (T), has the model structure: Y = A + T + AT + S'(A) + S'(A)T. Graphically, Y against time has one line for each treatment, joining means for successive intervals. The treatment effect is tested with S'(A) error MS, but T and AT are tested with S'(A)T error MS.
v) Analysis of covariance for experimental designs with both categorical and continuous explanatory variables. Tests a dependent variable for homogeneity among categorical group means, after using linear regression procedures to adjust for the groups' differences in the independent and continuous covariate (S&R p. 509; see Newman 1991 for appropriate uses and assumptions).
vi) General linear models for analysis of experimental and observational data. Glms can handle non-orthogonal designs and mixtures of continuous and categorical explanatory variables. Recommended also for unbalanced designs (not all treatment combinations contain the same number of variates). In a design with interactions, use sequential sums of squares to test the significance of main effects. Look for differences between sequential and adjusted sums of squares that indicate non-orthogonality.
2. Nonparametric
Assumes independence of data. Cannot mix categorical and continuous variables.
a) One-way analysis of variance
i) Kruskal-Wallis test for the general case of a samples and ni variates per sample (S&R p. 429).
ii) Jonckheere test for ordered alternatives (Sie p. 216) to test for rank order of group means.
iii) permutation test for two independent samples (Sie p. 151) tests for significance of the difference between the means of two independent samples of small size. Provides an exact probability without making any special assumptions about the underlying distribution in the population involved.
iv) Mann-Whitney U-test for two samples (=Wilcoxon's two-sample test, which is numerically equivalent to a permutation test based on ranks). H0: the two samples come from populations having the same distribution (S&R p. 432). Looks specifically for a difference in location. This is a rank test, distribution free and scale invariant.
v) Kolmogorov-Smirnov two-sample test of differences in the distributions of two samples of continuous observations. The test is sensitive to differences in location dispersion, skewness etc. Based on the unsigned differences between the relative cumulative frequency distributions of the two samples (S&R p. 440).
b) Two-way analysis of variance
i) Friedman's method for randomised blocks (Sie p. 174) in lieu of two-way anova. Non-parametric two-way tests cannot deal with a mixture of categorical and continuous response variables.
ii) permutation test for paired replicates (Sie p. 95) and Wilcoxon's signed-ranks test (=permutation test on ranked samples) in lieu of paired samples t-test (S&R p. 447-449).
ANALYSIS OF FREQUENCIES (1 sample)
1. Goodness-of-fit
a) Chi-squared and G-tests analyse frequency data for single
classification goodness-of-fit of a sample to a theoretical distribution
preferably of a nominal variable (S&R p. 704). H0:
observed frequencies are consistent with the theoretical distribution or
expected proportions (e.g. testing randomness of data, may be rejected if
p < 0.05, giving 95% certainty that the data are not randomly
distributed; or Mendel's dihybrid cross giving p > 0.9). William's
correction for G (S&R p. 704). Correction for continuity for
chi-squared test when a =2 and n <200, because discrete
frequencies are being tested against a continuous 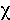 2
distribution (S&R p. 710; for n <25 use expected probabilities of
the binomial). Regroup classes or use an exact test of the multinomial
distribution when the number of classes a > 5 and the smallest
expected frequency is < 3 and for a < 5 and smallest expected
frequency is < 5 (S&R p. 709). Remember to subtract an extra degree of
freedom for each parameter in an intrinsic hypothesis that was estimated from
the sampled data (a - 3 for normal, a - 2 for Poisson
distributions: S&R p. 713).
2
distribution (S&R p. 710; for n <25 use expected probabilities of
the binomial). Regroup classes or use an exact test of the multinomial
distribution when the number of classes a > 5 and the smallest
expected frequency is < 3 and for a < 5 and smallest expected
frequency is < 5 (S&R p. 709). Remember to subtract an extra degree of
freedom for each parameter in an intrinsic hypothesis that was estimated from
the sampled data (a - 3 for normal, a - 2 for Poisson
distributions: S&R p. 713).
b) Kolmogorov-Smirnov one sample test is applicable to the case of a continuous frequency distribution without tied values, where it has greater power than the G- or chi-squared tests (S&R p. 716). It is especially advantageous for small sample sizes, when it is neither necessary nor advisable to lump classes. For large samples can also be used as an approximate test of data grouped into a frequency distribution (S&R p. 718).
c) Binomial test calculates exact probabilities of the binomial (S&R p. 70) for the hypothesis that an expected ratio is true for an observed pair of values. For example, from 17 offspring the probability (two-tailed) of obtaining a deviation from the hypothetical 1:1 sex-ratio as large or larger than 14:3 is 0.0127. For an observed ratio of 14:3 one or more of the following assumptions is therefore unlikely: i) that the true sex-ratio is 1:1; ii) that sampling was random in the sense of obtaining an unbiased sample; iii) that the sexes of the offspring are independent of one another (e.g. a sex-ratio may be equal on average, while individual litters are largely unisexual). Use exact probabilities instead of chi-squared when n < 25.
2. Independence in two-way tables
Tests a sample for interaction between the frequencies of two variables. Assumes truly categorical data, and independent frequencies (the occurrence of an event of type ij is not influenced by the type of the preceding event). Usually it should be subjects that are being classified, so the sample size (totals in a contingency table) is given by the number of subjects. See Kramer, M. & Schmidhammer, J. (1992) Anim. Behav. 44:833-841.
a) Chi-squared and G-tests analyse frequency data for independence (or
randomness) in two-way tables of categorical data (S&R p. 745).
H0: row and column classifications are independent (e.g. that
sex does not depend on residence time may be rejected if p < 0.05).
William's correction for G (S&R p. 745). Correction for continuity
(chi-squared) in 2x2 tables, because discrete frequencies are being tested
against a continuous 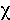 2 distribution (S&R p. 743; but
unduly conservative even for low n = 20, S&R p. 743). The cells with
fexp < 3 (when a
2 distribution (S&R p. 743; but
unduly conservative even for low n = 20, S&R p. 743). The cells with
fexp < 3 (when a  5) or
fexp < 5 (when a < 5) are generally lumped with
adjacent classes so that the new fexp are large enough; use
an exact test if this is not possible. Degrees of freedom =
(columns-1).(rows-1). Arrange large tables a priori according to
supposed gradients, and partition the degrees of freedom to find where the
important discrepancies are (Sie p. 194). Look also at residuals (but note that
they are not independent) which for large N have corresponding probabilities
following the normal distribution. (Sie p. 197). For tables with very large
n, a significant result is almost certain, because no two distributions
can be identical. Thus the distribution of ratios in the different columns must
vary at least slightly from row to row, and large counts allow these small
differences to be identified as significant. The problem is not with the test,
but with the hypothesis, which conveys little new information if rejected when
based on a large sample. For 2x2 tables, find confidence intervals for the Risk
ratio, following B.J.R. Bailey (1987) Biometrics 43:201. The limit
closest to unity corresponds to a Z-test of H0: ratio
= 1.
5) or
fexp < 5 (when a < 5) are generally lumped with
adjacent classes so that the new fexp are large enough; use
an exact test if this is not possible. Degrees of freedom =
(columns-1).(rows-1). Arrange large tables a priori according to
supposed gradients, and partition the degrees of freedom to find where the
important discrepancies are (Sie p. 194). Look also at residuals (but note that
they are not independent) which for large N have corresponding probabilities
following the normal distribution. (Sie p. 197). For tables with very large
n, a significant result is almost certain, because no two distributions
can be identical. Thus the distribution of ratios in the different columns must
vary at least slightly from row to row, and large counts allow these small
differences to be identified as significant. The problem is not with the test,
but with the hypothesis, which conveys little new information if rejected when
based on a large sample. For 2x2 tables, find confidence intervals for the Risk
ratio, following B.J.R. Bailey (1987) Biometrics 43:201. The limit
closest to unity corresponds to a Z-test of H0: ratio
= 1.
b) Fisher's exact test, of a 2x2 table where marginal totals are fixed for both criteria, is based on the hypergeometric distribution (equivalent to the binomial but sampled from a finite population without replacement) with 4 classes. This test answers the following question: given two-way tables with the same fixed marginal totals as the observed one, what is the chance of obtaining the observed cell frequencies and all cell frequencies that represent a greater deviation from expectation? H0: row and column classifications are independent. If an H1 predicts the direction of dependency then the one-tailed probability is appropriate, otherwise two-tailed, giving a truer probability on small samples than a 2x2 chi-squared or G-test (Sie p. 103).
c) phi coefficient for a measure of association in 2x2 tables that preserves direction; a special case of Pearson's correlation coefficient (Con p. 184-187).
d) Randomised blocks for frequency data: repeated testing of the same individuals or testing of correlated proportions (S&R p. 767). The previous methods were tests of the effect of treatments on the frequency of some attribute, where each treatment was applied to a number of independently and randomly selected individuals that were different for the separate treatments. Sometimes it is not possible or desirable to collect data in that manner. Where the same sample of individuals is exposed to two or more treatments, and we wish to test whether the change in proportion between the two trials is significant, use Cochran's Q-test.
e) Log-linear models for contingency tables. Uses a generalised linear model with a log link function to test whether column ratios vary from row to row (whether interaction is present between row and column categories). Can use more than two variables. e.g.: column * row * table = _response_ .
ANALYSIS OF ASSOCIATION BETWEEN 2 VARIABLES (1 sample)
1. Correlation
The interdependence or covariance of two variables. The existence of an interdependent relationship does not signify a functional relationship (S&R p. 561).
a) Pearson's product-moment correlation coefficient assumes a bivariate
normal distribution. Correction for bias when n  42 (S&R p. 566).
Significance testing with t-test (S&R p. 584). For a one-tailed
test, F = (1+|r|)/(1-|r|), which is tested against
F
42 (S&R p. 566).
Significance testing with t-test (S&R p. 584). For a one-tailed
test, F = (1+|r|)/(1-|r|), which is tested against
F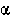 (1),
(1),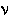 ,
,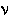 (
(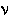 =
n-2).
=
n-2).
b) Spearman's rank correlation coefficient is a nonparametric measure. Equivalent to a product-moment correlation on the ranked variates.
2. Regression
For analysis of functional relationships between continuous variables (parametric: S&R p. 454; nonparametric: Con p. 263-271).
a) Linear regression. Significance of the regression slope is tested with an anova (S&R p. 467), where F = MS[regression] / MS[error] at 1 and n-2 degrees of freedom. Confidence limits to slope of regression line (S&R p. 473, 475); confidence limits to regression estimates (S&R p. 474, 476).
b) Regression forced through the origin. See Seber (1977) pp. 191-192.
c) Polynomial regression, to partition the sums of squares into linear and quadric components etc. Adjusted sums of squares are not appropriate in polynomial regression, due to considerations of marginality.
d) Logistic regression for a response variable comprised of proportional data and continuous or categorical dependent variable(s). For example:
failures/subjects = density
ANALYSIS OF ASSOCIATION BETWEEN >2 VARIABLES (1 sample)
1. Multiple correlation
a) Coefficient of multiple correlation (S&R p. 660).
b) Coefficient of partial correlation (S&R p. 656).
c) Kendall's coefficient of concordance on ranked variables (S&R p. 607).
2. Multiple regression
For ordinal independent variables. Problems of interpretation arise if the effects are strongly non-orthogonal (compare sequential and adjusted sums of squares). Model formulae constructed as for anova (S&R p. 618).
a) Comparison of regression lines (S&R p. 499) in Y on X1 for different levels of X2 is equivalent to testing for interaction effects in anova.
b) Stepwise procedure for post-hoc analyses (S&R p. 663).
3. Principal components analysis
A method of partitioning a resemblance matrix into a set of orthogonal components. Each pca axis corresponds to an eigenvalue of the matrix; the eigenvalue is the variance accounted for by that axis. Pca is a dimension-reduction technique, useful if the independent variables are correlated with each other, and there are no hypotheses about the components prior to data collection. Pca is a linear model: the co-ordinates of a sample unit in the space of the pca axes system are determined by a linear combination of weighted species abundances. Detrended pca is suitable for moderately non-linear data structures common in community ecology.
4. Discriminant functions
A topic in the general area of multivariate analyses, dealing with the simultaneous variation of two or more variables. It is used to assign individuals to previously recognised groups (dependent variables) on the basis of a set of independent variables. The analysis assesses whether group membership is predicted reliably. Assumes the response variables are multinormally distributed (S&R p. 683).
5. Multivariate analysis of variance
Used for evaluating differences among centroids for a set of dependent variables when there are two or more levels of an independent variable (one-way; factorial manova is the extension to designs with more than one independent variable). The technique asks the same questions as for discriminant function analysis, but turned around, with group membership serving as the independent variable.
6. Canonical ordination
Used for exploring the relationship between several response variables (e.g. species) and multiple predictors (e.g. environmental variables). Canonical correspondence analysis escapes the assumption of linearity and can detect unimodal relationships between species and external variables.
RESAMPLING METHODS
1. Randomisation test
A powerful nonparametric tool for situations where the data do not meet the assumptions required for customary statistical tests, or where we know little or nothing about the expected distribution of the variables or statistics being tested. Randomisation tests involve three steps: i) Consider an observed sample of variates or frequencies as one of many possible but equally likely different outcomes that could have arisen by chance; ii) enumerate the possible outcomes that could be obtained by randomly rearranging the variates or frequencies; iii) on the basis of the resulting distribution of outcomes, decide whether the single outcome observed is deviant (i.e. improbable) enough to warrant rejection of the null hypothesis. Probabilities of the binomial and Fisher's test are examples of exact randomisation tests based on probability theory. For examples of exact and sampled randomisation tests based on enumeration see S&R p. 790-795. Sampled randomisation tests belong to the general category of Monte Carlo methods of computer simulation by random sampling to solve complex mathematical and statistical problems.
2. Jackknife
A general purpose technique useful for analysing either a novel statistic for which the mathematical distribution has not been fully worked out or a more ordinary statistic for which one is worried about the distributional assumptions. It is a parametric procedure that reduces the bias in the estimated population value for a statistic and provides a standard error of the statistic. The idea is to repeatedly compute values of the desired statistic, each time with a different observed data point being ignored. The average of these estimates is used to reduce the bias in the statistic, and the variability among these values is used to estimate its standard error (S&R p. 795).
3. Bootstrap
A similar technique to the Jackknife. It involves randomly sampling n times, with replacement, from the original n data points to generate an independent bootstrap sample, from which to calculate the bootstrap replication of the statistic of interest (a ratio say). Repeating this procedure a large number of times, to have say 1000 replicates, then provides information on the characteristics of the statistic, such as its confidence intervals.
Book Sources
Arthurs, A.M. (1965). Library of Mathematics: Probability Theory. Routledge.
Conover, W.J. (1980). Practical Nonparametric Statistics (2nd ed.). Wiley, N.Y.
Crawley, M.J. (1993). Methods in Ecology: GLIM for Ecologists. Blackwell Scientific
Dobson, A.J. (1990). An Introduction to Generalized Linear Models. Chapman and Hall.
Grafen, A. (1993). Quantitative Methods Biology Final Honours School, University of Oxford. Lecture notes.
Ludwig, J.A. & Reynolds, J.F. (1988). Statistical Ecology: A Primer on Methods and Computing. John Wiley.
Newman, J.A. (1991). Notes on experimental design (2nd ed.). Lecture notes.
Parker, R.E. (1979). Introductory Statistics for Biology (2nd ed.). Studies in Biology no. 43. Edward Arnold, London.
Seber, G.A.F. (1977). Linear Regression Analysis. Wiley.
Siegel, S. & Castellan, N.J.Jr. (1988). Nonparametric Statistics for the Behavioral Sciences (2nd ed.). McGraw-Hill, New York & London.
Snedecor, G.W. & Cochran, W.G. (1980). Statistical Methods (7th ed.). Iowa State University Press.
Sokal, R.R. & Rohlf, F.J. (1981). Biometry (2nd ed.). Freeman.
Tabachnick, B.G. & Fidell, L.S. (1989) Using Multivariate Statistics. Harper.
Programs written in BBCBasic(86) by C.P.Doncaster, unless otherwise stated
AOV BPG 2,000 15/06/88 12:07 BONFERRO BPG 945 18/08/93 18:11 BOX_COX FOR 5397 25/04/92 20:21 CALC BPG 7,296 23/05/90 17:41 CHI BPG 5,320 20/10/88 10:24 CHR$CHAR BPG 848 01/08/91 14:09 CONTIN BPG 3,602 03/12/93 13:53 CONVERT BPG 830 18/11/89 15:47 COR BPG 6,780 01/11/88 12:56 CURVE BPG 1,210 23/01/89 12:19 DISTRIB BPG 9,133 07/03/91 11:41 DRIFT BPG 13,715 18/06/90 12:34 DYNAMIC BPG 10,540 26/01/95 18:33 EDI BPG 6,127 14/11/89 16:31 ESP BPG 2,852 16/11/92 14:39 EXACT BPG 1,871 30/10/88 18:08 FISHER BPG 2,180 21/10/88 17:02 GENEALOG BPG 2,416 09/03/94 18:57 GLOBE BPG 10,046 25/08/95 22:19 GLOBERAN BPG 8,348 03/11/95 15:59 INCIDEN BPG 10,077 11/08/95 14:20 ITERAT BPG 1,229 07/03/94 12:55 JACKNIFE BPG 3,715 17/09/93 18:22 LINEDIS BPG 7,971 25/02/93 13:41 MONTECAR BPG 5,908 05/07/88 17:07 NORMAL BPG 1,276 20/08/95 18:35 PASCAL BPG 837 27/06/88 17:22 PERIOD FOR 6931 25/03/91 14:21 PERM BPG 2,914 16/04/90 12:39 PERMII BPG 1,796 13/04/90 14:27 PI BPG 1,444 21/01/89 1:14 POLYGON BPG 1,460 15/06/88 10:20 PRIME BPG 730 15/07/95 0:45 RANFILE BPG 4,284 26/08/92 20:29 SETRISE BPG 4,661 05/05/93 14:47 STATIC BPG 13,361 26/01/95 18:31 T-TEST BPG 2,190 22/05/89 10:28 TABLES BPG 2,695 08/07/88 18:33 TILES BPG 4,745 29/01/92 13:49 VAR BPG 3,402 15/06/88 11:37 Z-TEST BPG 3,543 20/08/95 14:46
AOV One-way analysis of variance, giving a value of Fobs, and the mean, standard deviation and n for up to 26 groups. Reads observed data from a file created by EDI, one value for each group per line, groups arranged from largest to smallest n left to right (separated by commas or spaces).
BONFERRO Does a sequential Bonferroni test on P- values from tables of statistical tests, following Rice (1989) Evolution 43: 223- 225. Can assume component tests are independent.
BOX_COX Does Box-Cox transformation on individual data points or data grouped into frequencies. [Program in Fortran from listing in Krebs (1989) Ecological Methodology.]
CALC General purpose calculator employing all the mathematical functions available with basic. Up to 10 memories, sub-calculator, constant function, and copy last line. [Developed from program listing supplied by M-Tec Soft.]
CHI Analyses frequency data for single classification goodness of fit to a theoretical distribution, or independence in two-way tables. Chi-squared and G-tests are performed on any number of frequencies up to a 15 by 15 contingency table. For large contingency tables gives standardised residuals for each cell, and will perform a partitioning analysis to find out where in the table lie the most important discrepancies. Input the data column by column. [Partitioning modified from program supplied by Siegel & Castellan (1988) Nonparametric Statistics for the Behavioral Sciences.]
CHR$CHAR Lists all the CHR$ characters from 32 to 254.
CONTIN An exact test for an N x M contingency table. The computation can be based on the hypergeometric or the multinomial distributions, with four classes. [Program from listing in Wells, H. & King, J.L. (1980) Bull. Southern California Acad. Sci. 79: 65- 77.]
CONVERT For converting an ASCII file (*.TXT) to a corresponding Basic file (*.BDT) such as those created by EDI.
COR Calculates correlation coefficients and plots regression estimates. Significance of regression slope is tested with an analysis of variance, significance of product-moment correlation coefficient with a t-test (gives same P). Will provide confidence limits to the regression slope and estimates of y (with confidence limits) for a chosen x. Axes may be transformed, or ranked for a Spearman's correlation coefficient. Will test for equivalence in up to five regression slopes with an analysis of variance. Reads co-ordinates from files created by EDI, with one x and y per line. Will output a file of ranked variates.
CURVE Calculates the geodetic distance between two points of latitude and longitude. Uses the average Earth's radius of 6367.4 km; gives an error of up to 100 m in 600 km at the equator (0.017%).
DISTRIB Tests goodness of fit of observed data to the following frequency distributions:
1. normal (continuous, defined by classes marking off regular intervals);
2. Poisson (discrete, 0,1,2,3... occurrences);
3. truncated negative binomial (discrete, no zero value);
4. Poisson and truncated negative binomial (no zero value).
Plots frequency data and employs chi-squared and G-test, and Kolmogorov-Smirnov test for normal distribution. Reads observed data from a file created by EDI, one frequency per line. For the normal distribution data can be in one of two forms:
1. One frequency per line, starting and finishing with frequencies outside the limits of the first and last class marks; or
2. Actual measurements (up to 50), one per line in any order.
DRIFT Calculates the size of a home-range by the grid-cell method, and tabulates changes in the utilisation of grid-cells with time, following Doncaster (1990) J. theor. Biol. 143: 431-443. Will plot the home-range between any chosen dates. Reads timed co-ordinates from a file output from a database in ASCII format, or output from EDI, one line per fix and fixes in sequential order.
DYNAMIC For two animals tracked simultaneously, calculates minimum separation distances within time-blocks of a given width, accounting for a given independence interval, and uses non-parametric methods to test the strength of dynamic interaction, following Doncaster (1990) J. theor. Biol. 143: 431-443. Reads timed co-ordinates from a pair of files output from a database in ASCII format, or output from EDI, one line per fix and fixes in sequential order.
EDI A data editor allowing you to create and modify a file of any length and containing numbers and/or characters. It works on two levels: command (identified by *) and data input (identified by line number). Commands include input, list or store data; search for a character string; move to a chosen line; erase or modify lines; append another file; check available memory; leave program. Type `H' for a full list of the command keys. To change from command mode to data input type `I', and to leave data input press <enter> twice in succession. A few of the programs described here use data entered from a file created by EDI (AOV, COR, DISTRIB, MONTECAR, VAR).
ESP Puts up series of random numbers or symbols (colours, shapes, herb names) on the screen, and records their occurrence and order.
EXACT Binomial test, giving the exact probability from the binomial distribution that an expected outcome (one-tailed) or ratio (two-tailed) is true for an observed pair of values. An estimate of the two-tailed probability could also be obtained from the chi-squared distribution but would not be accurate for N < 25. Confidence intervals for a proportion can be obtained from the cumulative binomial probabilities given by specifying the two frequencies as 0, N.
FISHER An exact test of independence in a 2x2 contingency table with fixed row and column totals. The computation is based on the hypergeometric distribution with four classes. Gives the probability of obtaining the observed cell frequencies, plus all cell frequencies (for the same marginal totals) that represent more extreme outcomes in the same direction (one-tailed) or in either direction (two-tailed).
GENEALOG Models the build up of a population with time, starting from the lifetime output of one adult. Numbers of offspring per adult are randomly assigned up to a designated maximum. The genealogical tree is drawn for a designated number of generations. The productivity of a given generation can be adversely affected by a natural disaster which increases the risk of juvenile deaths, and thus the numbers of lines going extinct.
GLOBE Draws a globe on a perspective projection to any scale (up to a 1° window) with latitudes and longitudes at specified intervals. The globe can be tilted and swivelled to give any desired orientation. Plots and outputs geodetic distances between any two co-ordinates of latitude and longitude. Latitudes and longitudes can be input interactively, or read from an ascii file of form:
Ident dd.mm.yy hh:mm:ss ##.###N ###.###E [##.###N ###.###E ] c mass
GLOBERAN Draws a globe on a perspective projection to any scale (up to a 1° window) with latitudes and longitudes at specified intervals. The globe can be tilted and swivelled to give any desired orientation. Generates consecutive random co-ordinates at geodetic distances with specified mean and standard deviation from each other, and specified standard deviation from the chosen origin. Set standard deviations to the default 108 for completely random movement around the globe.
INCIDEN Models the persistence of a metapopulation, before and after random removal of a specified number of habitable patches. Patches are distributed at random within a specified rectangular area (anything from square to linear), and can vary in size at random within specified limits. The yearly incidence of occupied and unoccupied patches is obtained from the incidence function (Ji) proposed by I. Hanski (1994, J. Anim. Ecol. 63:151), with or without a rescue effect. Ji is a function of the extinction probability (Ei which depends on patch size) and the colonisation probability (Ci which depends on patch isolation with respect to dispersal behaviour). Four model parameters need to be specified to characterise Ei and Ci :
y' takes small values for good colonisers, little affected by isolation;
x decreases with increasing environmental stochasticity;
µ sets Ei = 1 for patch area  µ1/x
(critical patch area);
µ1/x
(critical patch area);
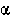 sets the survival rate of migrants over distance
dij.
sets the survival rate of migrants over distance
dij.
The program will iterate a value of 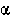 (or failing that, of y') that
approximates the requested percent occupancy. Graphical output is stored in a
file called `inciden.txt' in the default directory. The impact on persistence
of habitat removal as revealed by the model is discussed in C.P. Doncaster
et al. (1996) Oikos (in press).
(or failing that, of y') that
approximates the requested percent occupancy. Graphical output is stored in a
file called `inciden.txt' in the default directory. The impact on persistence
of habitat removal as revealed by the model is discussed in C.P. Doncaster
et al. (1996) Oikos (in press).
ITERAT Iterative procedure for solving equations such as:
0 = 3a6 + 7.1a4 - 0.9
(gives a = ±0.57735027)
Searches for a in both positive and negative regions within a specified range, and provides answer to specified accuracy.
JACKNIFE Uses Tukey's Jackknife method to compute the standard error for a sample statistic applied to up to 50 variables and 200 observations. The following options (described in PROCstat, using SUM values) are available:
1. Product- moment correlation coefficient on C1 and C2. Jackknife is on the z transformation of r (Sokal & Rohlf 1981 Biometry, p. 796).
2. Test of equality of two variances u=ln(SD1/SD2).
3. Index of dispersion ID=ln(variance/mean).
LINEDIS Calculates distance of co-ordinates from lines, and compares with a restricted random distribution of simulated co-ordinates, which can be repelled from, or attracted to, `den-sites'. Inputs reference files of observed fixes, den-site fixes and expected lines, the latter being in the form of an output from TILES.
METAMOD Models site transitions in a stochastic system. Creates n populations of random initial sizes between 1 and sj, and generates d dispersal/fidelity events between them under specified conditions described by three types of constraint:
1. Dispersal propensity: all populations have an equal and random probability of producing / receiving a migrant, or all individuals have an equal and random probability of emigrating, or all individuals have an equal and random probability of emigrating / immigrating;
2. Proximity: migration frequencies inversely proportional to distance between them with populations distributed around a circle, or no proximity effect;
3. Carrying capacity: unsaturated system with no limit on density, or density capped at sj + c , or saturated system with density remaining at sj, so each immigration into j provokes an emigration from j.
Each run produces r(1): log emigrant events against log immigrant events, r(2): log dij verses log dji, and r(3): log population size verses arcsine emigrant proportion. Output correlations are stored in `metamod.out' in the default directory, and raw data in `metamod2.out'.
MONTECAR Exact and sampled randomisation tests based on enumeration of a given statistic (STAT). Plots the frequency distribution for k items taken Y at a time, and gives the percentage of occurrences more deviant than the observed value of STAT. For a sampled test, the true level of significance for the entire population has probability limits given by running program EXACT on the sample percent. You must define the function (DEFPROCfunction) that will compute the STAT for your data set. The program includes two sample procedures, calculating the distinctness value for a k.k table of correlations, and calculating the variance for a sample size Y and its counterpart (k-Y) (following Sokal & Rohlf 1981, p. 790-794, with their data in files MONTECR1.BDT and MONTECR2.BDT). It may take several hours to run. Reads data from a file created by EDI, into a one-dimensional array X.
NORMAL Constructs a normal distribution from random numbers, using a specified
variance around a mean of zero. Values Y distant from the origin occur
with probability
Z =
e-(Y-µ)2/(2 2)
/ [
2)
/ [
 (2
(2 )]. Each Yi is obtained by
repeatedly generating a random distance Yij with its
corresponding probability Z(Yij), and a random number
Rj (0
)]. Each Yi is obtained by
repeatedly generating a random distance Yij with its
corresponding probability Z(Yij), and a random number
Rj (0  Rj
Rj  1/
1/
 (2
(2 )) until the first occurrence of
Z(Yij)
)) until the first occurrence of
Z(Yij)  Rj, which indicates an
acceptable Yi. As the distribution of all
Yi builds up, the tails rapidly become fixed and the `bell'
gets taller, but relative areas under the graph remain the same (e.g. 95% of
the area lies within 1.96
Rj, which indicates an
acceptable Yi. As the distribution of all
Yi builds up, the tails rapidly become fixed and the `bell'
gets taller, but relative areas under the graph remain the same (e.g. 95% of
the area lies within 1.96 ).
).
PASCAL Calculates C(k,Y) the number of combinations that can be formed from k items taken Y at a time. Will also show Pascal's triangle down to 23 levels.
PERIOD Does fourier transform periodogram to estimate significant harmonic components in time-series. [Uses program listing in Bloomfield (1976) Fourier Analysis of Time Series: an Introduction.]
PERM Permutation test for testing the significance of the difference between the means of two independent samples when sample sizes are small. The test employs the numerical values of the scores and therefore requires at least interval measurements. Determines the exact probability associated with the observations under the assumption of no difference between the means. [Optimised from program listed in Siegel & Castellan (1988) Non-Parametric Statistics for the Behavioral Sciences.]
PERMII Permutation test providing an exact probability of the difference between paired replicates of a small sample. [Optimised from program listed in Siegel & Castellan (1988).]
PI Calculates  to ± 1 in the last decimal place (up to 252 decimal
places of accuracy).
to ± 1 in the last decimal place (up to 252 decimal
places of accuracy).
POLYGON Plots a polygon and calculates its area, using a list of co-ordinates of adjacent vertices. For concave polygons start with a vertex that can make a straight line to all the others without passing outside the polygon. Program PLOT is recommended for more complicated polygons and calculation of perimeter vertices from numerous co-ordinates.
PRIME Lists all prime numbers between specified limits.
SETRISE Calculates sunrise and sunset UT at sea level from latitude, longitude and date. Corrects for sun's semi- diameter and refraction. Reads an output file from GLOBE to give azimuth and elevation. [Algorithm for sun's transit, azimuth and elevation from R. Walraven (1978) Solar Energy, 20: 393- 397; notation from Whittaker's Almanac (1993).]
STATIC Uses the grid-cell method, with influences if desired, to estimate the sizes of two home ranges and their area of overlap, and Spearman's r as a comparative index of static interaction between utilisation distributions, following Doncaster (1990) J. theor. Biol. 143: 431-443. The program reads timed co-ordinates from a pair of files output from a database in ASCII format, or output from EDI, one line per fix and fixes in sequential order.
T-TEST Uses sample size, mean and a variation parameter (SD, SE or variation) to test the hypothesis that two sample means come from the same population mean. Incorporates Bartlett's test of homogeneity of two or more variances, and an approximate test for the case of unequal variances. (For raw data use program AOV.)
TABLES Gives percentage points (± 1 in the 4th decimal place) for the following distributions:
1. F-distribution (inaccurate for > 30 d.f. among groups, or only 1 error d.f.).
2. Student's t-distribution (inaccurate for 10 > observed value > 100, with 1 d.f.).
3. Chi-squared distribution (inaccurate for observed value < 1, with 1 d.f.).
4. Normal distribution.
TILES Draws Dirichlet tiles around points. Takes an input file (x,y,f) or specified number of random points. Dirichlet lines can be output for use in LINEDIS. (CTILES produces coloured tiles.)
VAR Plots the histogram of a set of frequency data, and provides the mean, sample standard deviation, population variance, coefficient of variation, standard error of the mean. Can read in a data file created by EDI if desired.
Z-TEST For proportions that are not too small, gives confidence intervals for
the Risk ratio: the ratio of two proportions. Uses Method C in D. Katz et
al. (1978) Biometrics 34:469, and a generalisation of this method,
suitable for small sample sizes, proposed by B.J.R. Bailey (1987)
Biometrics 43:201. The value of Z from the test of significance
for the 2x2 contingency table then corresponds to one of these confidence
intervals approximating unity. Note that Z2 =
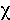 2 with 1 d.f., so the Z-test itself has no
advantages over a 2x2 chi-squared, indeed Z has no correction for
continuity when sample sizes are not equal.
2 with 1 d.f., so the Z-test itself has no
advantages over a 2x2 chi-squared, indeed Z has no correction for
continuity when sample sizes are not equal.
See also the Lexicon of Evolutionary Genetics.